Asturias4Steam

Metodologías

Publicado el 19 de Julio de 2024

I.Diego 19/07/2024

Descubrimos los principales elementos de la metodología Thinking Classroom con dos expertos en la materia: Luis José Rodríguez Muñiz, coordinador del Mathematics Education Research Group de la Universidad de Oviedo y Gregorio Morales Ordóñez, profesor de matemáticas que lleva años aplicando esta metodología en el IES Marjana (Chiva, Comunidad Valenciana).

Luis José y Gregorio son viejos conocidos de Asturias4STEAM. En Enero compartimos micrófono en el programa de radio que dedicamos a hablar de ansiedad matemática. En una de sus intervenciones hicieron mención a este enfoque metodológico propuesto por el investigador canadiense Peter Liljedahl y nos quedamos con ganas de saber más . Este es el fruto de una conversación a tres bandas que mantuvimos cuando el curso escolar estaba dando sus últimos coletazos.

Empecemos por el principio ¿de donde surge la metodología Thinking Classroom?

LJ: “Peter Liljedahl es un investigador canadiense que llevaba tiempo analizando su propia práctica y las prácticas de otros profesores de Matemáticas y se daba cuenta de que había un peso demasiado grande de las normas de la clase y sobre todo que el tiempo que el alumnado estaba pensando en clase de Matemáticas era nulo o prácticamente despreciable en muchos casos.”

GM: “En Norteamérica hace tiempo que la educación matemática tiene un enfoque más o menos por descubrimiento, creando entornos propicios para que alumnas y alumnos reflexionen para construir el conocimiento matemático. Así, no es de extrañar que se investigara qué valores tienen que tener ciertos parámetros para conseguir maximizar el tiempo de «pensamiento», entendido como los procesos matemáticos. Parámetros como ¿grupos de 2, de 3, de 4? ¿Sentados o de pie? ¿Soporte borrable o no borrable? ¿Influye todo esto en el tiempo que los alumnos y alumnas están pensando? Y dando respuesta a todas estas preguntas es como nace la metodología Thinking Classroom.”

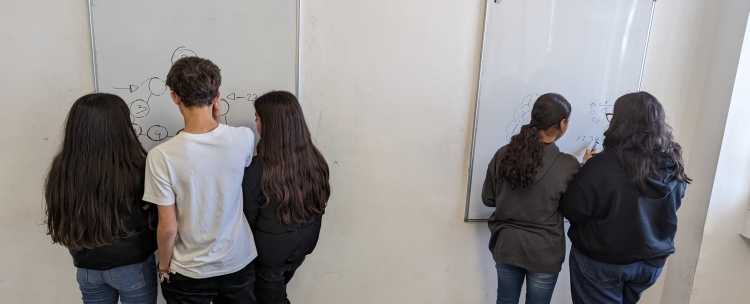
Alumnado de 1ºESO en un aula organizada bajo los principios de Thinking Classroom (IES Marjana)

¿Qué se encontraría una persona al entrar en un aula organizada bajo los principios de un Thinking Classroom?

LJ: “Pues a un montón de gente de pie, moviéndose, escribiendo en pizarras verticales, pensando y hablando mucho. Una clase donde es muy probable que nadie esté haciendo lo mismo porque cada grupo está trabajando por su cuenta, se mueve, habla, discute, se enfrenta a un problema y hay muchísima más actividad y se hace mucho más patente que la gente está pensando. Puede ser un poco caótica para quién le guste el orden porque rompe también la estructura de la clase.”

GM: “Si entras en una clase mía a mitad lo que más sorprendería es el escándalo: gente discutiendo sobre matemáticas, resolviendo conflictos y llegando a conclusiones. Y eso, la inmensa mayoría de las veces no se puede conseguir en silencio.“

Liljedahl menciona en uno de sus artículos que esta metodología supone una “ruptura violenta” con lo que todos entendemos por una clase de matemáticas. ¿Por qué es necesaria esta ruptura?

LJ : “Es una ruptura en el sentido de que se rompen las normas de la clase. ¿Por qué? Porque lo que nos dice la observación es que estas normas son las que nos están llevando precisamente a lo que queríamos evitar, que el alumnado esté en clase sin pensar. No piensas porque sabes que pasado un tiempo llegará el profesor y te dará la solución, y lo único que te interesa es copiarla. No piensas porque en el examen no te van a pedir pensar sino que reproduzcas algo parecido a lo que ya has hecho. No hablas con tus compañeros, porque las normas de clase no está bien visto que lo hagas. No intentas resolver un problema porque no se trata de que pienses como resolverlo sino de dar la solución correcta. No te atreves a dar una idea porque tienes miedo a que no sea la adecuada. Este tipo de normas son las que llevan a que en clase no se piense y que sea necesario romperlas.“

¿Qué supone esa ruptura a nivel de aula?

GM: “Bueno, supone una ruptura en diferentes niveles. En primer lugar, supone reducir la instrucción directa a su mínima expresión (cero en algunos casos) y eso ya es una ruptura con los enfoques más tradicionales. En segundo lugar, el papel del profesorado es totalmente distinto si se pretende no que repitan lo que tú haces y sabes hacer, sino que lo descubran por sí mismos con sus propias técnicas: hay que aprender a mantener la boca cerrada y que la guía consista sobre todo en hacer buenas preguntas. En último lugar, si el día a día en el aula no tiene un esquema de «yo hago-tú repites» entonces la evaluación no puede ser igual. Es una ruptura en todos los sentidos.”

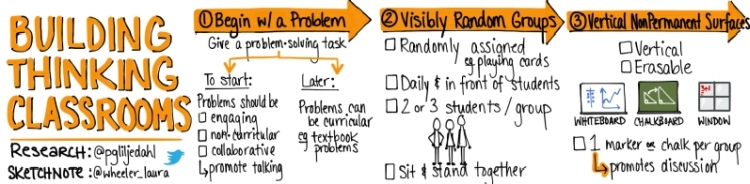
Tres principios clave: 1) Partir de un problema; 2) Grupos visiblemente aleatorios; 3) Superficies verticales que se puedan borrar

La resolución de problemas ocupa un lugar central en la propuesta de Liljedahl pero la palabra “problema” parece adquirir un significado totalmente diferente al de los problemas que encontramos en los libros de texto ¿En qué sentido?

GM: “Los libros de texto rara vez contienen problemas. Si bajo el epígrafe «Potencias de la misma base» aparece el enunciado de un problema raro será que no se resuelva aplicando la propiedad del producto de potencias de la misma base. Y eso no es un problema, es un ejercicio para practicar. Cuando no sabes qué hacer, ¡entonces tienes un problema!”

LJ: “Con respecto a la distinción entre un ejercicio y un problema hay mucha bibliografía al respecto. Un problema tiene que ser algo que te reta, que te genera un conflicto. En los problemas tienes que primero pasar un rato viendo de qué va y luego buscando la forma de resolverlo. No se trata tanto de identificar el procedimiento que tengo que aplicar, por ejemplo una integral, sino de ver cómo lo puedo hacer. Por lo tanto es algo que lleva tiempo y que emocionalmente va a tener mucha incidencia porque me puede generar bloqueos, ansiedad, frustración cuando no encuentre la solución o alegría cuando lo haga. Involucra mucho más emocionalmente a la persona que se enfrenta a su resolución. Además al contrario que un ejercicio, un problema se plantea de forma más abierta, tengo que tomar decisiones sobre lo que estoy resolviendo, llegar a acuerdos sobre qué características vamos a simplificar o complejizar para resolverlo. Un problema no es de resolución inmediata, emocionalmente me involucra, está poco definido y además puede tener más de una solución correcta.“

Alumnado resolviendo de problemas sobre superficies verticales no permanentes

Otro aspecto que salta inmediatamente a la vista es la ausencia mesas y sillas desaparecen de la vista. ¿Qué aporta que el alumnado trabaje de pie?

GM: “La diferencia es brutal y es difícil explicarlo si no lo has visto en directo. El hecho de que el equipo esté de pie hace que se enfrenten juntos al problema como una piña. Además, permite al profesorado una visión de 360° para tener una noción mucho más completa de lo que está ocurriendo en clase.”

LJ: “Esto parte de cuestiones relacionadas con lo socio-afectivo. Pensar que el alumnado tiene que estar quieto en una mesa 5-6 horas al día es muy difícil. El movimiento beneficia a los pre-adolescentes y adolescentes porque es una forma de liberar estrémuscular y relajarse. Por otro lado, desde el punto de vista de las matemáticas estar de pie supone romper las normas de la clase y hace que estén más activos. Otra cuestión adicional es que es más fácil ver lo que tú haces y lo que hacen los demás. Es más fácil moverte y comparar lo que estás haciendo con el resto de los equipos.”

¿Y eso de dejar los cuadernos, pantallas y pizarra para revestir las paredes del aula con superficies en las que se puede escribir y borrar continuamente?

LJ: “Lo del borrar también está bastante estudiado en la bibliografía y tiene parte de base en el valor sacrosanto que se le da al cuaderno y las notas por tenerlo inmaculado cuando en Matemáticas es precisamente lo contrario. El cuaderno tiene que estar sucio, nadie aprende linealmente y bien a la primera sino que aprendes equivocándote. Es esa parte socio-afectiva de darle valor al error como método de aprendizaje. Entonces el hecho de que tu puedas borrar hace que te atrevas a escribir mucho más, a intentar hacer más cosas.”

La metodología Thinking Classrooms plantea la creación de equipos de estudiantes de forma visiblemente aleatoria. ¿Qué quiere decir esto? ¿Son equipos estables?

LJ: “En este sentido la metodología es tajante. Tienen que ser equipos visiblemente aleatorios. Es decir, que el alumnado vea que cada día se hacen equipos diferentes. De este modo se va minando a medio plazo esos roles que se establecen en clase de este es el listo, este es el tonto. También cambia dentro del grupo quién se encarga de escribir para que no sea uno el que coja el boli y lo haga todo.”

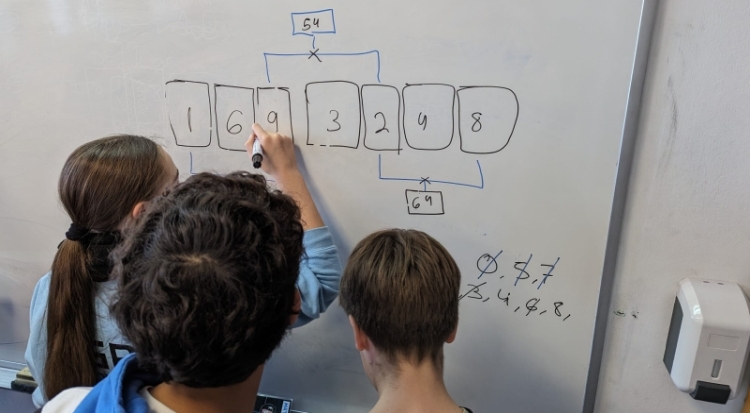
Equipos de tres que se forman de manera visiblemente aleatoria al principio de cada sesión.

¿Cómo se crean estos equipos y cuál es el tamaño adecuado?

GM: “En el libro Building Thinking Classrooms se dice que los grupos deben ser de 3 personas y que se deben crear de forma visiblemente aleatoria. Así es como se fomenta de manera más eficiente el diálogo y la negociación. Si los ponemos en grupos de 4 corremos el riesgo de que las discusiones se hagan por parejas en paralelo sin puesta en común. Estos grupos son visiblemente aleatorios en cada sesión. Yo lo hago con una baraja de cartas que te indica a qué pizarra has de ir. Así, tras contar el problema, reparto las cartas y se ponen a trabajar. “

Entonces todos los días se rehacen los equipos ¿qué ventajas tiene esto?

GM: “El hacerlos aleatorios tiene dos grandes ventajas. La primera, que se reduce notablemente el stress asociado a «yo quiero ir con fulanito y menganita» o «¿por qué me has puesto con fulanito?», ya que al hacerlo aleatorio nadie es responsable de ese azar y se asume rápidamente. La segunda ventaja es la de permeabilizar el conocimiento y permitir que las técnicas y estrategias que se van descubriendo se vayan «contagiando» por toda la clase al cabo de dos o tres sesiones.“

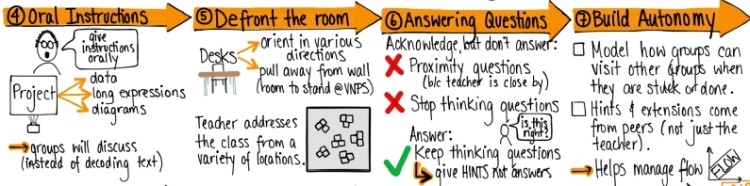
El papel del profesorado en un Thinking Classroom: Dar pistas no respuestas.

Los problemas a los que se enfrentan no tienen una única solución y esta incertidumbre genera muchas preguntas dirigidas al profesorado para saber si van por el buen camino ¿cómo se gestiona esto en el aula?

LJ: “La metodología es muy clara. Nosotros queremos que el aula sea un aula para pensar por tanto sólo se responden aquellas preguntas que ayudan a seguir pensando. De este modo, Liljedahl distingue varios tipos de preguntas. Aquellas preguntas que sólo se hacen cuando el profesor está cerca y no me oyen los demás. Esas no se responden, se dan evasivas o se contestan con otras preguntas. Tampoco se responden aquellas de “Profe ¿voy bien?”. Sólo se responden aquellas preguntas que tengan relación con el problema a resolver. Y la forma es responder planteando otra pregunta, buscando paralelismos, devolviendo la pregunta a otro alumno haciendo que contrasten diversas aproximaciones. Ese es otro pilar de esta metodología. Si tu vas diciendo vas bien, vas mal, se acabó. Vuelves a lo que se intentaba evitar desde el principio que es que la gente no piense porque sabe que tú le vas a dar la solución.“

Morderse la lengua no resultará fácil para el profesorado al principio.

GM: “Eso también se gestiona aprendiendo qué clase de preguntas no tienes que responder y cuáles sí. Y cuando es que sí, hay que aprender a responder con otra pregunta. A este respecto, el libro Questions and Prompts for Mathematical Thinking de Anne Watson y John Mason es una maravilla que todo docente debería leer.”

¿Es fácil detectar si los alumnos están realmente pensando?

GM: “Se ve a kilómetros a distancia. Y si encima se acostumbran, como es el caso, a que te acerques a la pizarra y compartan contigo en voz alta lo que están pensando pues se observa mejor todavía. Es con el diálogo estudiante-estudiante y estudiante-profesor como se construye el discurso matemático y se ponen en marcha las competencias matemáticas.”

LJ: “Así es. Ves mucha actividad, están discutiendo, están hablando, ves que la clase termina y quieren seguir pensando. ¿Y cuándo no? Pues cuando el problema es muy fácil y se acaba pronto o el nivel de dificultad es demasiado alto y la gente se atasca.”

También nos llama la atención que, por una vez, el carácter disruptivo de esta metodología no está asociado a la adopción de tecnologías sofisticadas y caras. De hecho, Liljedahl insiste en que los cambios en la práctica docente que plantea son fáciles de poner en marcha. Bajo vuestro punto de vista, ¿es realmente así? ¿con qué dificultades os habéis encontrado?

LJ: “Puede ser complicada la gestión del espacio porque a veces no se presta a mover sillas y mesas particularmente en aquellas aulas donde están atornilladas al suelo y por lo tanto queda muy poco espacio en vertical para trabajar. Caro, no es caro. Hay varias opciones muy asequibles que se pueden utilizar como superficies verticales: pizarras y film borrable, metacrilato, cristales.“

GM: ”A nivel de infraestructura es realmente sencillo y solo requiere voluntad. Yo he llegado a hacerlo aprovechando las ventanas del aula, y tengo compañeros que llevan rollos de vinilo blanco para colocar rápidamente en las paredes. Lo complicado es cambiar el chip acerca de qué es enseñar matemáticas, qué es aprender matemáticas, qué es hacer matemáticas, y qué significa evaluar.”

¿Cuál es el grado de implantación de este metodología en Asturies en comparación con otras CCAA?

LJ: “Hasta donde yo sé en Asturias tiene muy poca implantación. Me atrevería a decir que lo estamos usando en la Universidad de momento. Sé que hay alguna profesora que ha llevado a cabo alguna experiencia puntual pero no de manera sistemática. En otras comunidades hay algo más de gente como Gregorio en Comunidad Valenciana. Es algo que va poco a poco y funciona mucho el boca a oreja.”

GM: “En Valencia lo he visto implantarse en diferentes centros, pero siempre gracias a la voluntad de profesoras y profesores a nivel individual. Ahora estamos moviendo el tema para crear formación del profesorado desde la administración. A ver qué tal.”

Portada del libro Cómo plantear y resolver problemas (Polya, 1945)

La mera mención de la innovación metodológica genera rechazo entre parte del profesorado cansado quizás de asistir al desfile de ocurrencias tras las que no existe un mínimo sustento teórico que las apoye. ¿Qué les diríais a los escépticos?

LJ: “Yo les diría a los escépticos que es disruptivo pero de innovador tiene muy poco porque Polya allá por el año 1945 decía que vale más resolver un problema de cinco maneras diferentes que hacer cinco ejercicios iguales. Las matemáticas van de pensar, de enfrentarse a un problema, de aprender de tus errores, comparar con lo que piensan los demás, discutir y, al final, encontrar la solución. Por lo tanto esta metodología va al núcleo de la actividad matemática. Además tiene unos fundamentos teóricos que parten de de la revolución que supuso el libro How to solve it? [Cómo plantear y resolver problemas matemáticos] de Polya de resolución de problemas en los años 40. Además hay investigación empírica de aula que demuestra las afirmaciones que realiza Liljedahl y sustento proporcionado por evidencia que aunque no use exactamente Thinking Classroom si que usa algunas cuestiones relacionadas. Por lo tanto hay evidencia directa de Thinking Classroom y evidencias parciales de otras metodologías que recoge a su vez Thinking Classroom. “

¿Veis esta metodología transferible a otras materias?

GM: “Me cuesta visualizarlo por ser desconocedor de la didáctica específica de otras materias. Pero, por ejemplo, creo que es una metodología estupenda para la morfo-sintaxis. La reflexión de qué función tiene cada palabra en una oración se puede hacer empezando con oraciones sencillas y construyendo a partir de las reflexiones del alumnado sin apenas instrucción.”